Apr 01, 2019 tags: | exploratory analysis |
Follow-up on “How random can you be?”
I have collected thousands of data points (percentages of correct guesses) via Google Analytics. As expected, most visitors didn’t play past 100-200 key presses, and only the most dedicated players reached 1000 key presses.
| # of inputs | mean, % | # of points |
|---|---|---|
| 100 | 57.6 | 31,425 |
| 200 | 60.0 | 22,148 |
| 300 | 61.0 | 14,221 |
| 500 | 60.2 | 8,600 |
| 1000 | 57.6 | 3,792 |
The model appears to be most accurate (60-61%) at 200-500 key presses. It’s accuracy is noticeably lower at 100 key presses, which makes sense since it has to collect statistics on the frequency of 2^6=64 different patterns to make meaningful predictions. Curiously, the model accuracy also suffered at 1,000 key presses. My guess is those who played that long resorted to the help of the pseudo-random number generator.
Let’s compare the actual distributions of correct guesses with those expected for random inputs. Please note the actual data includes cases where visitors probed the algorithm with De Bruijn sequences and computer-generated pseudo-random numbers or fed it predictable patterns deliberately.
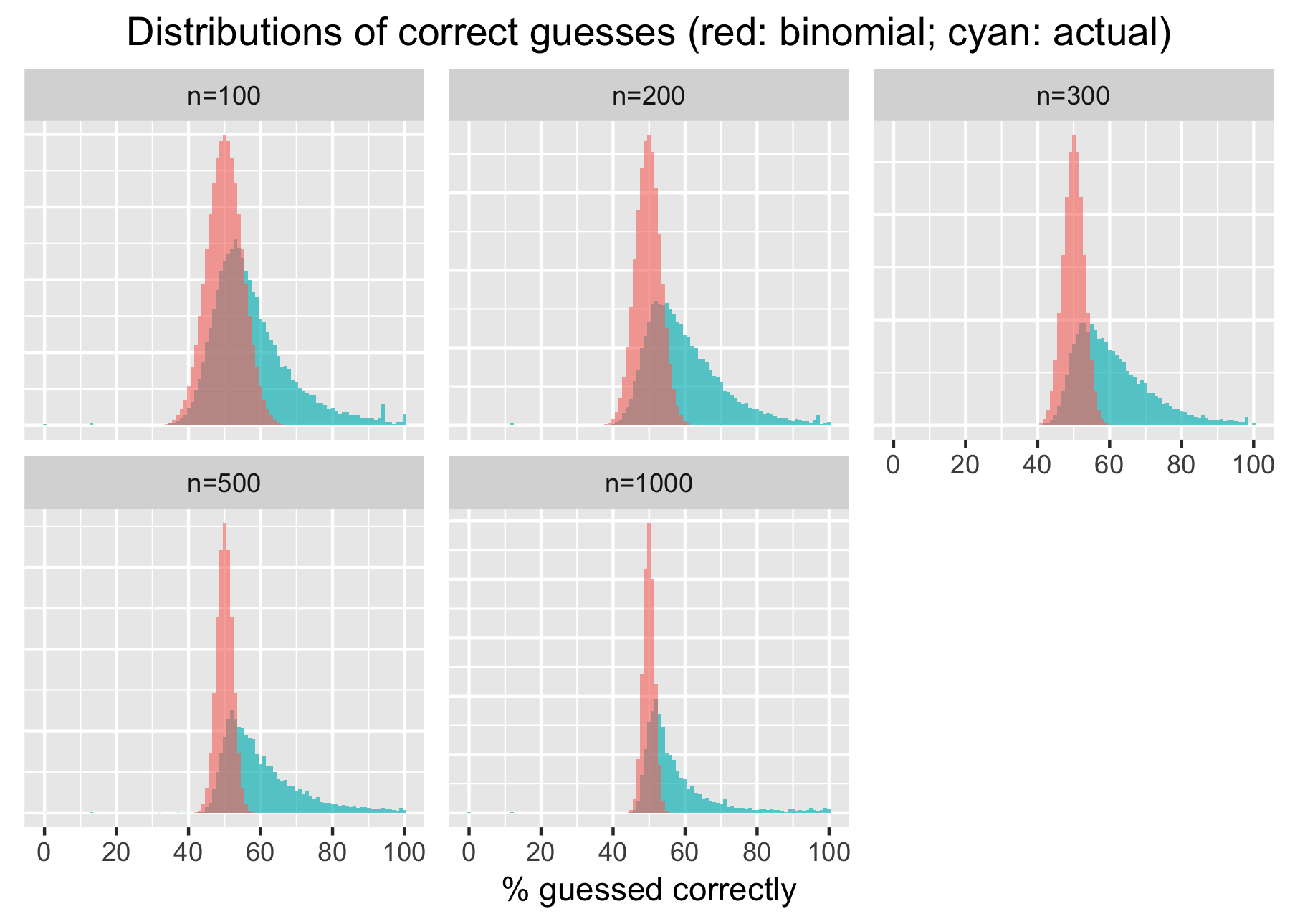
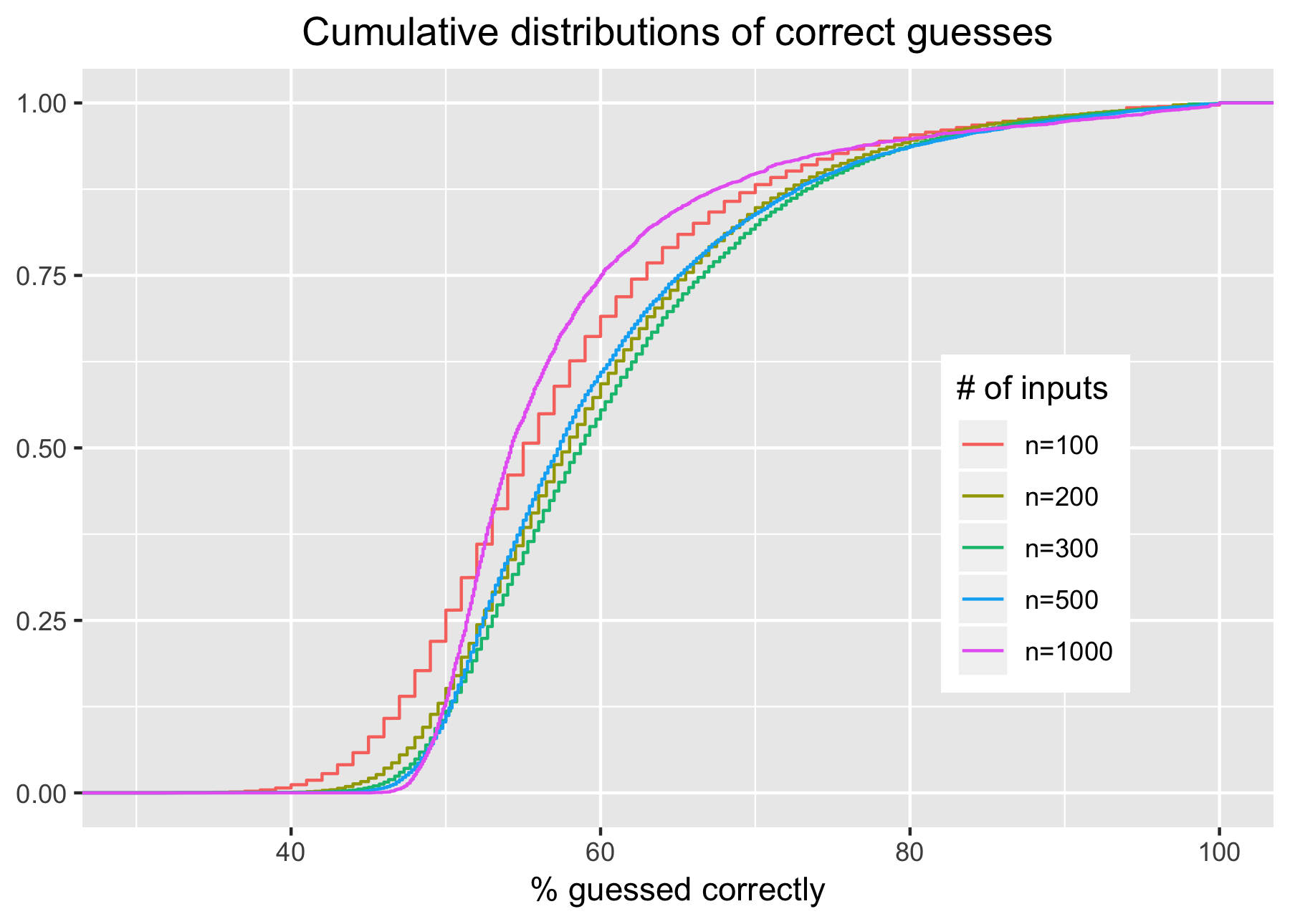
The following cumulative plots show that only a small percentage of players have less than 50% of their key inputs predicted correctly.
I used a predictor based on 6-grams (base length n = 5) becaused it seemed to give better results than shorter grams. However, as noted in the original post, I hadn’t been able to test other models thoroughly myself, so I decided to collect actual player inputs and use them to determine the effect of gram base length on model accuracy. Once again I used Google Analytics for data collection. Left was encoded as “0”, and right was encoded as “1”. Every group of 6 bits was converted into a byte which was incremented by 48 to produce a printable ascii character. At 180 iterations all characters were joined into a string (e.g., “EA?P2YAU87JZZX0<8GnZXN=FT5oe:5”) which was then passed to Google Analytics as an event. Since only actual player inputs were collected (i.e. no pseudo-random numbers), some strings ended up having fewer than 30 characters.
I noticed that many sequences contained repeated characters (for example, “e9EEZOEECoEEEEEEEEEEEjQB[B]:”). These characters represent easily predictable repetitions of 00, 01, 10, and 11. I searched and removed all instances of more than 9 of such repetitions in a row, and removed all sequences that ended up being shorter than 144 inputs. Thus I ended up with two sequence datasets: one containing everything that was collected, and the other one combed to keep only the less obvious patterns. I ran both datasets through models with various gram base lengths, and got the following results:




Surprisingly, the best performance was achieved with base length = 3. However, it’s important to keep in mind that this benchmark was obtained in a synthetic test where the virtual player didn’t get any feedback until the game was over. Real players try to outsmart the bot by keeping track of their inputs. 4-grams produce only 16 different patterns which aren’t difficult to remember. So after all 6-gram based prediction might work just as well (or even better) than shorter gram bases.
Suggested post:
Real time abstract art generation using a neural net
